Symbol Key, Inferences, and Equivalences

 

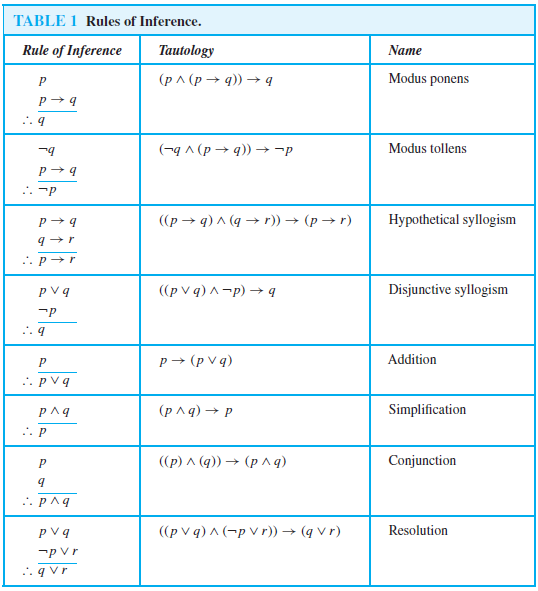
Law of inferences 

Here are the symbols of various logical operators as I use them on this website (there is no one, universal list of symbols, though certain norms are adhered to across the spectrum):

∧ = And

∨ = Or

→ = If…then

¬  = Not (negation)

≡   = Logical Equivalence

Here are the most common inferences in symbolic logic:

1) Modus Ponens (MP)

P → Q

P 

Therefore, Q

2) Modus Tollens (MT)

P → Q

¬Q 

Therefore, ¬P

3) Hypothetical Syllogism (HS)

P → Q

Q → R 

Therefore, P → R

4) Disjunctive Syllogism (DS)

P ∨ Q

¬P

Therefore, Q

5) Simplification (SIMP)

P ∧ Q 

 Therefore, P

6) Addition (ADD)

P 

Therefore, P ∨ Q

7) Double Negation (DN)

P 

 Therefore, ¬¬P

8) Conjunction (CONJ)

P

Q 

Therefore, P ∧ Q

9) Constructive Dilemma (CD)

(P → Q) ∧ (R → S)

P ∨ R 

Therefore, Q ∨ S

10) Destructive Dilemma (DD)

(P → Q) ∧ (R → S)

¬Q ∨ ¬S 

 Therefore, ¬P ∨ ¬R

Finally, here are the 9 logical equivalences:

1) De Morgan’s Theorem (DeM)

¬(P ∧ Q) ≡ ¬P ∨ ¬Q

¬(P ∨ Q) ≡ ¬P ∧ ¬Q

2) Commutation (Comm)

(P ∨ Q) ≡ (Q ∨ P)

(P ∧ Q) ≡ (Q ∧ P)

3) Association (Assoc)

[P ∨ (Q ∨ R)] ≡ [(P ∨ Q) ∨ R]

[P ∧ (Q ∧ R)] ≡ [(P ∧ Q) ∧ R]

4) Distribution (Dist)

[P ∧ (Q ∨ R)] ≡ [(P ∧ Q) ∨ (P ∧ R)]

[P ∨ (Q ∧ R)] ≡ [(P ∨ Q) ∧ (P ∨ R)]

5) Double Negation (DN)

¬¬P ≡ P

6) Transposition (TRANS)

P→Q ≡ ¬Q→¬P

7) Material Implication (IMP)

P→Q ≡ ¬P ∨ Q

8) Material Equivalence (Equiv)

P≡Q ≡ [(P→Q) ∧ (Q→P)]

P≡Q ≡ [(P ∧ Q) ∨ (¬P ∧ ¬Q)

9) Exportation (Exp)

[(P ∧ Q)→R] ≡ [P→(Q→R)]

10) Tautology (Taut)

P ≡ (P ∧ P)

P ≡ (P ∨ P)